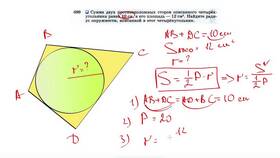
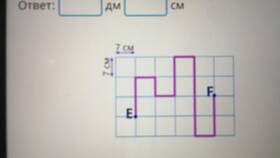
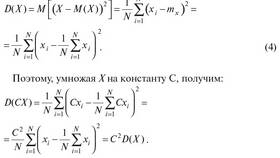Сумма противолежащих углов вписанного четырехугольника всегда равна 180 градусам. Это важное свойство вытекает из теоремы о вписанных углах и широко применяется в геометрических задачах.
Содержание
Формулировка теоремы
Во всяком вписанном четырехугольнике сумма противолежащих углов составляет 180°. Математически это можно выразить как: ∠A + ∠C = ∠B + ∠D = 180°.
Доказательство теоремы
- Рассмотрим вписанный четырехугольник ABCD с вершинами на окружности
- Проведем диагонали AC и BD
- Угол ABC опирается на дугу ADC
- Угол ADC опирается на дугу ABC
- Сумма этих дуг составляет полную окружность (360°)
- Следовательно, сумма углов ABC и ADC равна половине 360°, то есть 180°
Геометрическая иллюстрация
| Углы | Сумма | Графическое представление |
| ∠A + ∠C | 180° | Опираются на дополняющие дуги |
| ∠B + ∠D | 180° | Опираются на дополняющие дуги |
Практическое применение
- Определение возможности вписать четырехугольник в окружность
- Решение задач на нахождение неизвестных углов
- Доказательство свойств вписанных четырехугольников
- Построение геометрических фигур
Примеры решения задач
Пример 1: Нахождение неизвестного угла
В вписанном четырехугольнике ABCD известны углы: ∠A = 75°, ∠B = 105°. Найти ∠C и ∠D.
Решение: ∠C = 180° - ∠A = 105°; ∠D = 180° - ∠B = 75°
Пример 2: Проверка на вписанность
Можно ли вписать в окружность четырехугольник с углами 80°, 95°, 100° и 85°?
Решение: 80° + 100° = 180°; 95° + 85° = 180° ⇒ можно вписать
Обратная теорема
Если в выпуклом четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность. Это важный признак вписанного четырехугольника.
Особые случаи
| Четырехугольник | Свойство углов |
| Прямоугольник | Все углы по 90°, суммы пар 180° |
| Равнобедренная трапеция | Суммы противолежащих углов по 180° |
| Квадрат | Частный случай прямоугольника |
Заключение
Свойство суммы противолежащих углов вписанного четырехугольника является мощным инструментом в геометрии. Оно позволяет решать широкий класс задач и доказывать важные геометрические теоремы. Запомните, что если четырехугольник вписан в окружность, суммы его противолежащих углов всегда равны 180 градусам.