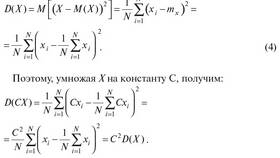Математическое ожидание суммы случайных величин является фундаментальным понятием теории вероятностей и имеет важное значение в статистическом анализе и прикладных исследованиях.
Содержание
Основное свойство математического ожидания суммы
Для любых случайных величин X и Y (как зависимых, так и независимых) выполняется следующее равенство:
- E[X + Y] = E[X] + E[Y]
- где E[·] обозначает математическое ожидание
Обобщение на произвольное число слагаемых
Свойство линейности математического ожидания распространяется на сумму любого конечного числа случайных величин:
- Для n случайных величин X₁, X₂, ..., Xₙ
- E[X₁ + X₂ + ... + Xₙ] = E[X₁] + E[X₂] + ... + E[Xₙ]
- Это верно независимо от зависимости между величинами
Пример вычисления
| Случайная величина | Математическое ожидание |
| X | 3 |
| Y | 5 |
| Z | -2 |
| X + Y + Z | 3 + 5 + (-2) = 6 |
Важные частные случаи
Для независимых случайных величин
- Хотя математическое ожидание суммы не требует независимости
- Для независимых X и Y: E[XY] = E[X]E[Y]
- Это свойство не распространяется на сумму
Для одинаково распределенных величин
- Если X₁, X₂, ..., Xₙ имеют одинаковое мат. ожидание μ
- Тогда E[X₁ + X₂ + ... + Xₙ] = nμ
- Это основа для оценки средних значений
Доказательство свойства линейности
Для двух дискретных случайных величин X и Y:
- E[X + Y] = ΣΣ (x + y)P(X=x, Y=y)
- = ΣΣ xP(X=x, Y=y) + ΣΣ yP(X=x, Y=y)
- = ΣxP(X=x) + ΣyP(Y=y) = E[X] + E[Y]
Применение в статистике
Это свойство широко используется в:
| Выборочных средних | E[Ȳ] = E[(Y₁+...+Yₙ)/n] = μ |
| Линейных моделях | E[aX + bY] = aE[X] + bE[Y] |
| Оценке параметров | Несмещенность оценок |