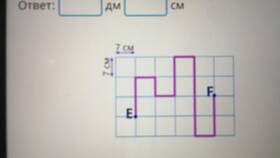
Сумма кубов чисел - это результат сложения кубов двух или более чисел. Для чисел a и b сумма кубов записывается как a³ + b³, где a³ = a × a × a и b³ = b × b × b. Это понятие широко используется в алгебре и теории чисел.
Содержание
Основное определение
Формула суммы кубов
| Тип формулы | Выражение |
| Для двух чисел | a³ + b³ = (a + b)(a² - ab + b²) |
| Для трех чисел | a³ + b³ + c³ - 3abc = (a + b + c)(a² + b² + c² - ab - bc - ca) |
Примеры вычислений
- 1³ + 2³ = 1 + 8 = 9
- 3³ + 4³ = 27 + 64 = 91
- 5³ + 6³ + 7³ = 125 + 216 + 343 = 684
Разложение на множители:
x³ + 8 = (x + 2)(x² - 2x + 4)
Применение суммы кубов
- Решение алгебраических уравнений
- Доказательство математических теорем
- Анализ числовых последовательностей
- Оптимизация в компьютерных алгоритмах
Исторические факты
| Период | Вклад |
| Древняя Греция | Изучение кубических чисел |
| Средние века | Разработка формул разложения |
| XVIII век | Доказательство теоремы Ферма для n=3 |
Интересные свойства
- Сумма кубов последовательных чисел связана с квадратом их суммы
- 1³ + 2³ + ... + n³ = (1 + 2 + ... + n)²
- Наименьшее число, представимое как сумма двух кубов двумя способами - 1729
Пример для последовательных чисел:
1³ + 2³ + 3³ = 36 = (1 + 2 + 3)² = 6²
Практическое значение
Сумма кубов находит применение в криптографии, компьютерной графике (3D-моделирование) и физике (расчет объемных характеристик). Понимание этого понятия важно для изучения высшей математики и прикладных наук.