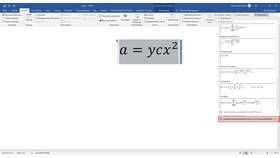
Вывод формул требует понимания основных принципов математического анализа и алгебры. Рассмотрим методику вывода различных типов формул.
Содержание
Основные методы вывода формул
| Метод | Применение |
| Аналитический вывод | Последовательные математические преобразования |
| Геометрический метод | Использование графических построений |
| Экспериментальный метод | На основе эмпирических данных |
Этапы аналитического вывода
- Постановка задачи и определение исходных данных
- Выбор математического аппарата
- Последовательное преобразование выражений
- Проверка размерности и предельных случаев
- Верификация результата
Пример вывода формулы квадратного уравнения
Исходное уравнение
ax2 + bx + c = 0
Выделение полного квадрата
- Деление на a: x2 + (b/a)x + c/a = 0
- Перенос свободного члена: x2 + (b/a)x = -c/a
- Добавление квадрата половины коэффициента: x2 + (b/a)x + (b/2a)2 = (b/2a)2 - c/a
Получение конечной формулы
x = [-b ± √(b2 - 4ac)] / (2a)
Правила преобразования формул
- Сохранение равенства при переносе членов
- Учет области допустимых значений
- Проверка эквивалентности преобразований
- Учет особенностей тригонометрических тождеств
Типичные ошибки при выводе формул
| Ошибка | Пример |
| Нарушение порядка операций | √(a+b) ≠ √a + √b |
| Некорректное применение свойств | ln(a+b) ≠ ln a + ln b |
| Потеря решений | Сокращение на переменную без учета нулевого значения |
Проверка правильности вывода
- Подстановка конкретных значений
- Анализ размерности
- Проверка предельных случаев
- Сравнение с известными результатами
Программные средства для работы с формулами
- LaTeX для набора сложных формул
- Mathematica для символьных вычислений
- Mathcad для численного анализа
- GeoGebra для геометрического вывода
Освоение техники вывода формул требует систематического подхода и понимания фундаментальных математических принципов.